讲座主题：Vertex stabilizers of symmetric graphs and their applications

主讲人： 郭松涛

工作单位：河南科技大学

活动时间：2020年12月13日 15:40-16:30

讲座地点：腾讯会议，会议ID：850 153 808

主办单位：烟台大学数学与信息科学学院

内容摘要：

A graph, with a group 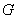of its automorphism, is said to be 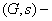transitive, if G is transitive on 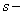arcs but not on 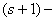arcs of the graph. Let X be a connected 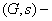transitive graph, and let 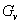be the vertex stabilizer of a vertex in 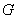. In 1980, Djokovic and Miller gave the exact structure of 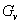for the cubic case, and Weiss and Potocnik gave such structure for the tetravalent case. In this talk, we will discuss the structure of 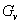for the pentavalent and hexavalent cases, and give the idea of the main proof. Also, with the similar method, we can get such structures for the valency 7 and 8.

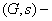  transitive graph is also simply called symmetric graph or arc-transitive graph. A graph is called edge-primitive if the full automorphism group of the graph is primitive on edges. The structure of the vertex stabilizer 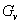plays an important role in the study of 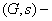transitive graph. As we all known that except for a star graph, all the edge-primitive graphs are arc-transitive. We will introduce the method about how to use the structure of 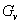to determine the edge-primitive graphs with small valencies, and also some symmetric graphs of certain order and valency.

主讲人介绍：

郭松涛，副教授。2009年广西大学硕士毕业，导师徐尚进教授。2012年北京交通大学博士毕业，导师冯衍全教授。现就职于河南科技大学-数学与统计学院，从事代数图论、置换群论和组合网络等方面的研究。主持国家自然科学青年基金1项，河南科技大学青年学术技术带头人培育项目1项。在J.Combin.Theory B, J. Algebraic Combin., Electronic J. Combin., Discrete Math., Algebra Colloquium, Acta Math. Appl. Sinica English Series等国内外著名期刊上发表论文30余篇.