Maxwell方程的电磁散射理论是反问题领域的研究难点，其成果在医学成像、雷达技术、无损探测等领域具有重要应用性。反问题的唯一性理论是依据测量数据唯一确定和反演未知物体的形状和位置的根本保障。单联通区域的Maxwell方程的反问题唯一性理论已经有较多研究结论，其研究主要聚焦于未知物体形状的反演。对于多联通复杂区域的Maxwell方程的反问题唯一性理论的研究一直是众多科研学者关注的难点问题。多层区域带来的散射叠加问题，埋藏物体的未知性以及Maxwell方程系统的复杂性都给问题的研究带来巨大的挑战，导致构造复几何光学解、构造爆破解等传统证明反问题唯一性的方法不能直接应用。

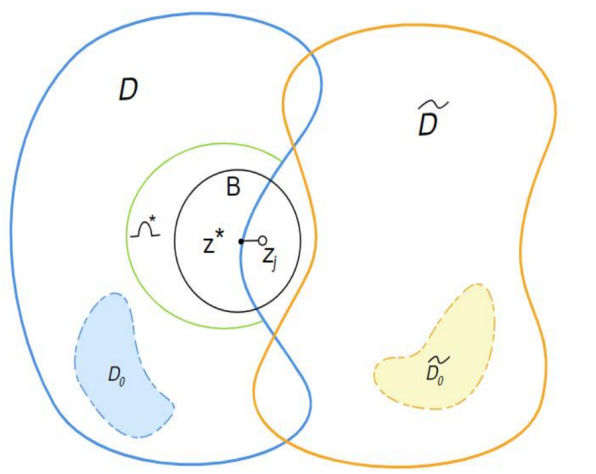
曲风龙团队首先利用变分方法研究了Maxwell方程正散射问题解的适定性，通过构造人工Maxwell系统，将问题转化为积分算子形式，利用积分方程方法构建了散射解在各个多联通区域边界附近区域的一致先验估计。基于散射解的一致先验估计，联合局部分析思想，形成了Maxwell系统的内部传输系统，分析得到了复杂介质形状和位置反演的唯一性理论。通过构造不同形态的PEC边界的Maxwell系统，证明了复杂介质传导系数反演的唯一性理论，其研究去掉了已有工作对于传导系数部分已知的先验假设。

相关成果以“Global uniqueness for determining an inverse electromagnetic scattering medium and its physicalcoefficients”为题发表于《Inverse Problems》（中国数学会1区，反问题领域顶级期刊），曲风龙为第一作者，研究生王玉博为第二作者，相关工作得到了国家自然科学基金、山东省自然科学基金的资助。

论文链接：https://libproxy.ytu.yitlink.com/https/443/org/iop/iopscience/yitlink/article/10.1088/1361-6420/ade61e